Charles Poussot-Vassal

Construction of a simplified model of a wave guide simulator (December 2024)

The Loewner framework, extended to port Hamiltoninan structures given by, $$ \left\{ \begin{array}{rcl} M\dot x(t)&=&(J-R)Qx(t)+(G-P)u(t) \\ y(t)&=&(G+P)^\top Qx(t)+(N+S)u(t) \end{array} \right., $$ is used to construct a simplified / reduced order dynamical model from data collected directly from a Maxwell's equation driven simulator. The reduced model recovers first the structure, second the input/output behavior and third, enable the full state (approximate) reconstruction.

The figure shows a wave guide simulation composed of three permittivity regions in response to an electric wave injected from the left. The magnetic (H, top) and electric (E, bottom) fields obtained by the expert simulator (in 10 minutes) and the reduced model (obtained in 1 second) are shown.

M. Gouzien, C. Poussot-Vassal, G. Haine and D. Matignon, "Port-Hamiltonian reduced order modelling of the 2D Maxwell equations", in journal for Computation and Mathematics in Electrical and Electronic Engineering (COMPEL).
>> ISAE Open Science

The multivariate Loewner framework : Taming the curse of dimensionality and the Kolmogorov superposition theorem (May 2024)

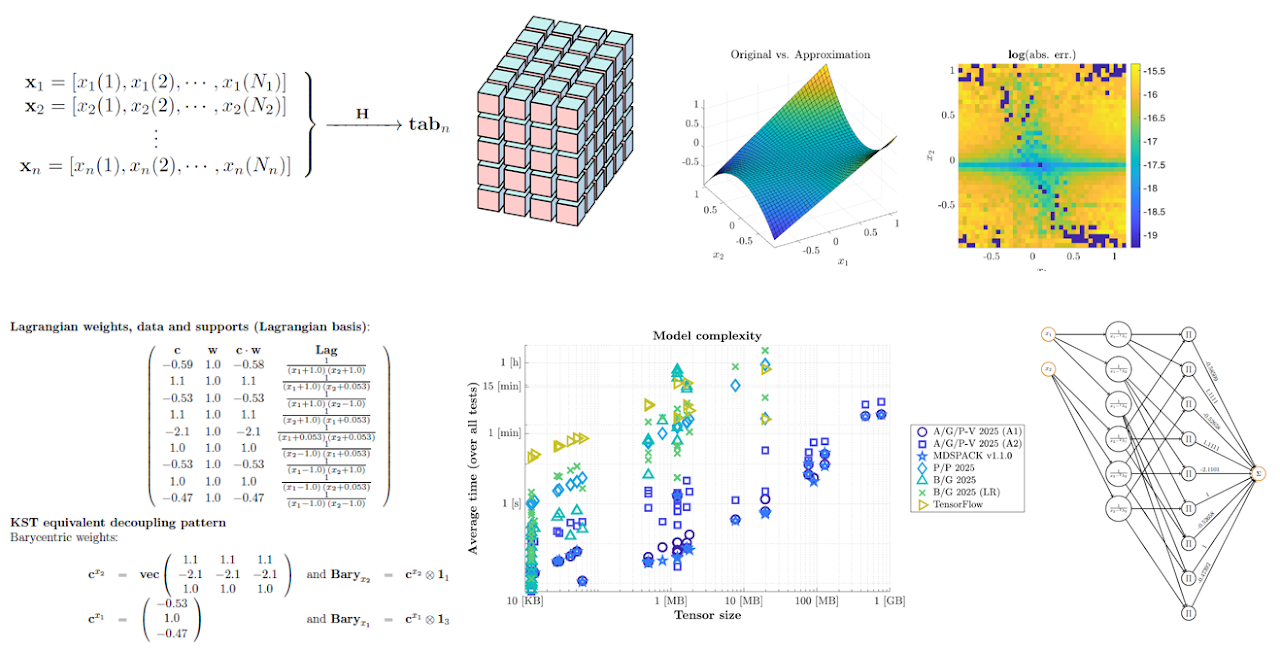
We propose a generalized realization form for rational functions in $n$-variables (in the Lagrange basis);
We show that the $n$-dimensional Loewner matrix is the solution of a series of cascaded Sylvester equations;
We demonstrate that the barycentric coefficients can be computed using a sequence of small-scale 1-dimensional Loewner matrices instead of the large-scale ($N \times N$) $n$-dimensional one, therefore drastically reducing the both computational effort and memory needs, and improving accuracy;
We show that this decomposition achieves variables decoupling; thus connecting the Loewner framework for rational interpolation of multivariate functions and the Kolmogorov Superposition Theorem (KST), restricted to rational functions. The result is the formulation of KST for the special case of rational functions;
Connections with KAN neural nets follows (detailed in future work).

$$ \begin{array}{ccl} \mathbb C^{k_1} \times\mathbb C^{q_1} \times \ldots \times \mathbb C^{k_n}\times \mathbb C^{q_n} \times \mathbb C^{(k_1+q_1)\times \cdots \times (k_n+q_n)} & \longrightarrow & \mathbb C^{Q\times K} \\ \left(\lambda^{(1)},\mu^{(1)},\ldots,\lambda^{(n)},\mu^{(n)},\texttt{tab}_n\right) & \longmapsto & \mathbb L_n \end{array} $$ where each entry of the $\mathbb L_n$ matrix reads $$ \ell_{j_1,j_2,\cdots,j_{n}}^{i_1,i_2,\cdots,i_{n}} = \dfrac{v_{i_1,i_2,\cdots,i_n}-w_{j_1,j_2,\cdots,j_n}}{(\mu^{(1)}_{i_1}-\lambda^{(1)}_{j_1})\cdots (\mu^{(n)}_{i_n}-\lambda^{(n)}_{j_n})}. $$

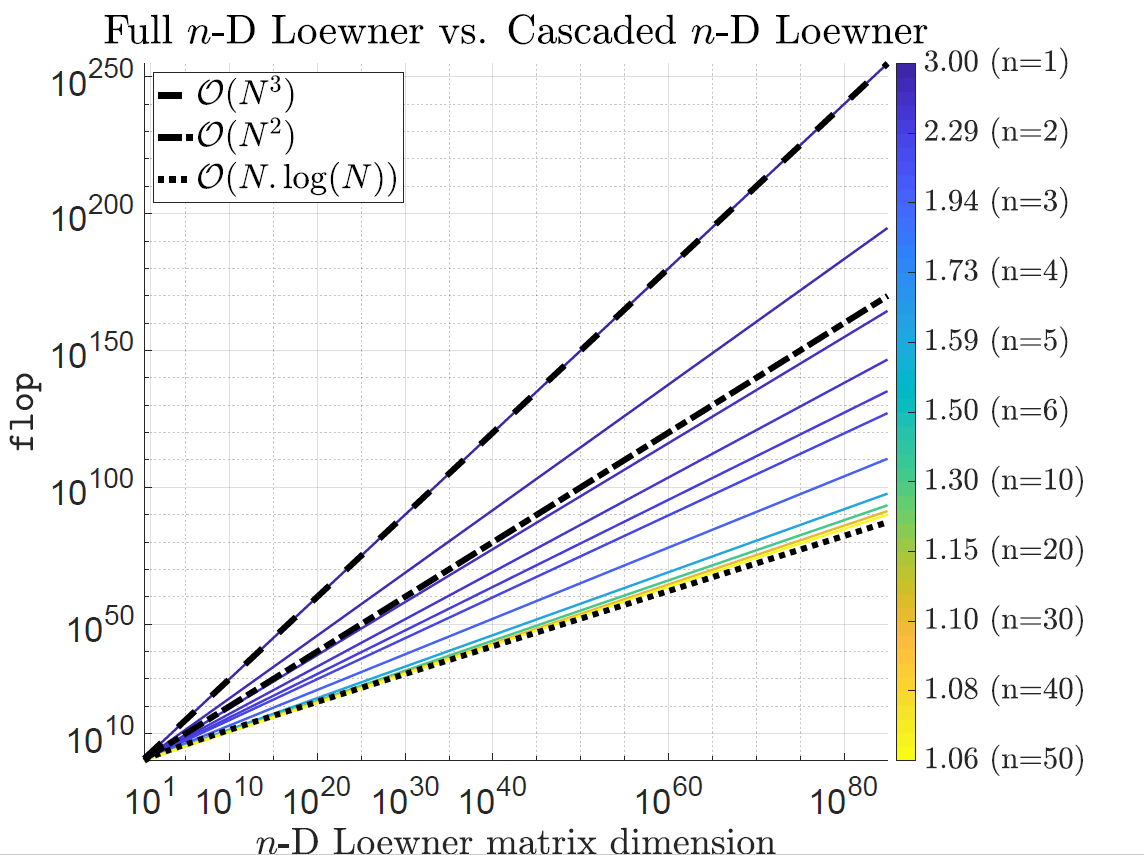
Figure compares flop: cascaded $n$-D Loewner worst-case upper bounds for varying number of variables $n$, while the full $n$-D Loewner ($\mathbb L_n\in \mathbb C^{N \times N}$) is $\mathcal{O}(N^3)$ (black dashed); comparison with $\mathcal{O}(N^3)$ and $\mathcal{O}(N \log(N))$ references are shown in dash-dotted and dotted black lines.

A. C. Antoulas, I. V. Gosea and C. Poussot-Vassal, "On the Loewner framework, the Kolmogorov superposition theorem, and the curse of dimensionality", in SIAM Review (Research Spotlight)
>> arXiv
>> GitHub code
>> video, recorded live on YouTube

Riemann zeta function zeros and prime counting function approximation (June 2022)

The realisation landmark of Mayo and Antoulas, through the lens of the modified Loewner framework is used to approximate the non-trivial zeros of the famous Riemann zeta function. These approximated zeros are then used to approximate the Riemann prime counting function, as illustrated in the right frame. $$ \pi(\lfloor x \rfloor ) \approx \mathbf{Ri}(x) - \sum_{\rho_{r}} \mathbf{Ri}(x^{\rho_r})- \sum_{\rho_{i}} \mathbf{Ri}(x^{ \rho_i}) =\mathbf J(x) $$ where $\rho_i$ are the non-trivial zeros or the $\zeta$ Riemann function $$ \zeta(z) = \displaystyle \sum_{n=1}^\infty \frac{1}{n^z}. $$

Figure compares of the prime counting function (thin red) with the Riemann formulae including non-trivial zeros approximated by the Loewner approach (solid blue). As the number of non-trivial (harmonics) zeros increases, the step shape is revealed.

C. Poussot-Vassal, I.V. Gosea, P. Vuillemin and A.C. Antoulas "Loewner framework for Riemann zeta function non-trivial zeros and prime counting function approximation", still in preparation.
>> slides

Non-intrusive nonlinear reduced order modelling of a pollutant dispersion (December 2020)

The non-intrusive MII (Mixed Interpolatory and Inference) procedure aims at constructing a nonlinear reduced order model (ROM) from time-domain input-output data issued from any complex simulator or measurements. The proposed process allows to construct a nonlinear ROM that accurately reproduce the complex simulation and that can be used for prediction, analysis. This ROM is a dynamical model of an appropriate structure.

Figure shows the horizontal cross section of pollutants concentration from four sources (red stars) with an eastward wind. Original data from complex simulator Large Eddy Simulation (LES, left), and nonlinear Reduced Order Model (ROM, right). The LES solution runs in 5,600 hours on a cluster while the ROM in seconds over a standard laptop.

C. Poussot-Vassal, T. Sabatier, C. Sarrat and P. Vuillemin, "Mixed interpolatory and inference non-intrusive reduced order modeling with application to pollutants dispersion", to be submitted.
>> arXiv

Data-driven control of a pulsed fluidic actuator (February 2020)

Illustration of the data-driven control design, applied on a pulsed fluidic actuator (PFA). PFA are typical on/off actuators that blow air in order to modify the pressure in a flow setup. They are typically used to control fluidic phenomena. The design is done using the Loewner-Data Driven Control (L-DDC) rationale.

Figure shows the considered closed-loop (top) and the performance in signal tracking obtained on the experimental tech bench (bottom). The photo is the top view of the PFA.

C. Poussot-Vassal, P. Kergus, F. Kerhervé and D. Sipp " Interpolatory-based data-driven pulsed fluidic actuator control design and experimental validation", in IEEE transaction on Control Systems Technology, Vol. 30(2), March 2022, pp. 852-859.
>> arXiv
>> video (closed-loop tracking performances of the PFA)

Vibration control demonstrator applied on a Dassault-Aviation Business jet
>> Ground Vibration Test (September 2015)
>> Flight tests (September 2017)

The vibration attenuation achieved on a Dassaut-Aviation Business Jet Falcon 7X has been done. To this aim, the MDSPACK library has been used to construct, from data, dynamical models of a Dassault-Aviation 7X. Then, a structured H-infinity controller has been designed to attenuate the vibration over a frequency-limited range.

Figure shows the Falcon 7X s/n 001 during ground vibration test.

C. Meyer, G. Broux, J. Prodigue, O. Cantinaud and C. Poussot-Vassal, "Demonstration of innovative vibration control on a Falcon Business Jet", in Proceedings of the International Forum on Aeroelasticity and Structural Dynamics (IFASD), Como, Italy, June, 2017.
>> video (experimental ground test)
>> video (interview)

Active gust load alleviation on an aeroelastic model (May 2015)

In the Onera wind tunnel facility, both trans- and sub-sonic configurations to attenuate gust load, have been obtained thanks to an advanced frequency-domain identification procedure based on data-driven model approximation performed with the MDSPACK library, followed by an active closed-loop control done in the structured H-infinity framework.

Figure shows the experimental set-up in the Onera S3Ch WT: aeroelastic airofoil (foreground) and gust generator (background).

>> video (slow motion, control "on" at 19 seconds)
>> Onera communication

Tensor-based multivariate function approximation: methods benchmarking and comparison (June 2025)